BSP-дерево и способы его применения в трехмерной графике

"Смотри в корень..."
К. Прутков

1. Что такое BSP-дерево

Обзор

     Binary Space Partitioning (BSP) дерево - стандартное бинарное дерево, используемое для сортировки и поиска многоугольников и многогранников в n-мерном пространстве. Взятое в целом BSP-дерево представляет собой все пространство, а каждый его узел ограничивает выпуклое подпространство. Каждый из узлов дерева хранит информацию о "гиперплоскости", делящей пространство узла на 2 части (переднюю и заднюю, что определяется направлением вектора нормали этой плоскости), а также ссылки на два новых узла, представляющих эти части. Заодно в узлах может храниться информация об одном или нескольких полигонах, лежащих в этой "гиперплоскости".
     Обычно BSP-деревья используются для представления двух- и трехмерных пространств, однако по определению эти структуры не ограничены тремя измерениями.

Пример

     Очень несложно разобраться с BSP-деревом, если ограничить нашу дискуссию двумя измерениями. Еще проще нам будет, если мы предположим, что используются только линии, параллельные осям X и Y, и что мы будем делить пространство на равные части для каждого узла.
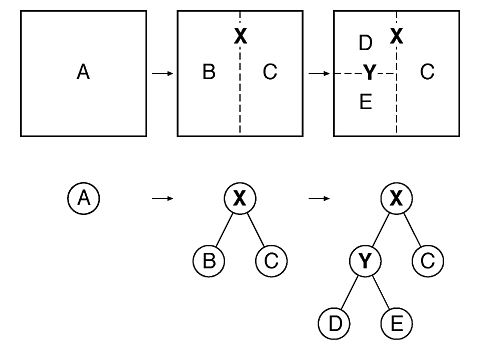
Рассмотрим такой пример (довольно стандартный): у нас есть квадрат где-то в плоскости XY.
     1. Мы производим первый раздел (который будет узлом нашего дерева). Разобьем квадрат пополам в направлении оси X.
     2. Для каждого рассечения мы будем изменять направление линии раздела на противоположное, т.о. второй "разрез" будет произведен над оставшимися секторами в направлении оси Y.
     3. Этот процесс можно продолжать рекурсивно, пока не будет достигнута "точка останова".
     Результат можно изобразить таким образом:

2. Как построить BSP-дерево

Обзор

     Итак, дано несколько полигонов в трехмерном пространстве. Задача: построить BSP-дерево, которое бы содержало их все. На данный момент нас не интересуют особенности построения дерева для каких-то специфических нужд.
     Алгоритм построения дерева очень прост:
     1. Выбрать делящую плоскость.
     2. Разделить полигоны (сцену или один объект) этой плоскостью, переслав многоугольники, находящиеся в полупространстве нормали делящей плоскости в положительную ветвь (предположим, правую), а остальные - в отрицательную (левую).
     3. Рекурсивно повторить для обоих получившихся узлов.

Выбор делящей плоскости

     Обычно эта плоскость выбирается в зависимости от того, как будет использовано дерево. Для некоторых целей лучше выбирать делящую плоскость из входящего списка полигонов (такой метод "у них" называется autopartition, у нас, наверно, авторазделение). Однако многие приложения могут только выиграть от выбора делящих плоскостей, параллельных осям.

Разделение полигонов

     Разделение списка полигонов делящей плоскостью производится путем определения положения каждого полигона из списка относительно плоскости. Если многоугольник полностью находится по одну сторону делящей плоскости, то он не модифицируется, а просто добавляется к одному из двух новых узлов дерева в зависимости от расположения этого полигона относительно плоскости (если он справа - то добавляется в правую ветвь и наоборот). Если же многоугольник пересекается делящей плоскостью, то он делится на две части, и каждая из них добавляется в свой узел (правая половинка - в правый, левая - в левый).

Когда остановиться

     Собственно, есть несколько критериев оценки необходимости завершения построения дерева (ого, как загнул!): оценка количества полигонов в узле, "прогон" всех многоугольников в дерево, достижение максимальной глубины дерева - в любом случае, выбор условия завершения зависит только конкретно от ваших и вашего приложения нужд.

Псевдокод

     Ну вот мы и подобрались к самому интересному - псевдокоду рекурсивной функции для создания BSP-дерева. Но сначала рассмотрим структуру, описывающую каждый узел дерева:

struct    BSP_tree
{
plane partition;
list polygons;
BSP_tree *front,
*back;
};

     Это определение структуры мы будем использовать для всех примеров. В ней хранятся указателя на дочерние узлы, делящая плоскость и полигоны, принадлежащие (лежащие в) этой плоскости. Для первого примера предположим, что в списке принадлежащих плоскости полигонов всегда только один многоугольник: тот самый, по которому мы и вычисляем делящую плоскость для этого узла дерева. Метод-конструктор для этой структуры должен инициализировать указатели на дочерние узлы в NULL:

void    Build_BSP_Tree (BSP_tree *tree, list polygons)
{
polygon *root = polygons.Get_From_List ();
tree->partition = root->Get_Plane ();
tree->polygons.Add_To_List (root);
list front_list,
back_list;
polygon *poly;
while ((poly = polygons.Get_From_List ()) != 0)
{
int result = tree->partition.Classify_Polygon (poly);
switch (result)
{
case COINCIDENT:
tree->polygons.Add_To_List (poly);
break;
case IN_BACK_OF:
back_list.Add_To_List (poly);
break;
case IN_FRONT_OF:
front_list.Add_To_List (poly);
break;
case SPANNING:
polygon *front_piece, *back_piece;
Split_Polygon (poly, tree->partition, front_piece, back_piece);
back_list.Add_To_List (back_piece);
front_list.Add_To_List (front_piece);
break;
}
}
if ( ! front_list.Is_Empty_List ())
{
tree->front = new BSP_tree;
Build_BSP_Tree (tree->front, front_list);
}
if ( ! back_list.Is_Empty_List ())
{
tree->back = new BSP_tree;
Build_BSP_Tree (tree->back, back_list);
}
}

     Эта процедура рекурсивно конструирует BSP-дерево используя приведенное выше определение. Она берет первый полигон из входящего списка и использует его для деления оставшихся. Потом процедура рекурсивно вызывает сама себя для деления обеих получившихся частей. Эта реализация алгоритма предполагает, что все многоугольники - выпуклые.
     Процедуру теоретически можно улучшить только одним способом - выбирать делящую плоскость более интеллектуально. Но:. это уже совсем другая история.

3. А как мне разделить полигон плоскостью?..

Обзор

     Разделение полигона плоскостью в основном заключается в определении по какую сторону он находится от секущей плоскости. Эта процедура обычно называется front/back test и производится путем проверки положения каждой вершины многоугольника относительно плоскости. Если все точки лежат по одну сторону, то весь полигон находится по эту сторону и нет необходимости его делить. Если же некоторые точки лежат по разные стороны плоскости, то многоугольник требует деления на две (или более) частей.
     Простейший алгоритм заключается в последовательном прохождении всех сторон полигона и поиске тех, вершины которых лежат по разные стороны плоскости. Потом вычисляются точки пересечения этих сторон с плоскостью и полученные значения используются как вершины для результирующих многоугольников.

Заметки по созданию алгоритма

     Определение положения точки относительно плоскости производится простой подстановкой координат точки (x,y,z) в уравнение плоскости Ax+By+Cz+D = 0. Результатом этой операции будет расстояние от точки до плоскости. Оно будет положительным, если точка находится по ту сторону плоскости, в которую указывает вектор нормали и отрицательным, если по другую. Если же результат равен 0, то точка лежит на плоскости.
Если вы ноль в математике и "уравнение плоскости" для вас - непроходимый лес, я поясню, что A, B, и C - это координаты вектора нормали, а D может быть заранее рассчитано подстановкой точки с координатами (x,y,z), лежащей в этой плоскости.
     Вообще выпуклые полигоны гораздо проще делить чем невыпуклые, так как первые всегда делятся на две выпуклых же части, а с последними иметь дело очень сложно, особенно если они самопересекающиеся.

Псевдокод

     Вот очень простая (но действующая) функция для разделения полигона плоскостью. Прошу заметить, что именно на эту функцию ссылается наш предыдущий пример:

void Split_Polygon (polygon *poly, plane *part, polygon *&front, polygon *&back)
{
int count = poly->NumVertices (),
out_c = 0, in_c = 0;
point ptA, ptB,
outpts[MAXPTS],
inpts[MAXPTS];
real    sideA, sideB;
ptA = poly->Vertex (count - 1);
sideA = part->Classify_Point (ptA);
for (short i = -1; ++i < count;)
{
ptB = poly->Vertex (i);
sideB = part->Classify_Point (ptB);
if (sideB > 0)
{
if (sideA < 0)
{
// вычисление точки пересечения линии
    // идущей от точки A к точке B с делящей плоскостью.
    // это простой алгоритм пересечения луча и плоскости
vector v = ptB - ptA;
real sect = - part->Classify_Point (ptA) / (part->Normal () | v);
outpts[out_c++] = inpts[in_c++] = ptA + (v * sect);
}
outpts[out_c++] = ptB;
}
else if (sideB < 0)
{
if (sideA > 0)
{
// вычисление точки пересечения линии
    // идущей от точки A к точке B с делящей плоскостью.
    // это простой алгоритм пересечения луча и плоскости
    vector v = ptB - ptA;
real sect = - part->Classify_Point (ptA) / (part->Normal () | v);
outpts[out_c++] = inpts[in_c++] = ptA + (v * sect);
}
inpts[in_c++] = ptB;
}
else
outpts[out_c++] = inpts[in_c++] = ptB;
ptA = ptB;
sideA = sideB;
}
front = new polygon (outpts, out_c);
back = new polygon (inpts, in_c);
}

     Вы, я думаю, уже заметили подвох в этом коде и вообще в алгоритме. Эта процедура делит треугольник не на два треугольника, а на треугольник и четырехугольник. Ну что же, если для вас важно сохранить все примитивы в своем мире треугольными, то есть следующие предложения по модернизации этой процедуры:
     1. В параметрах передавать указатель не на одну часть полигона а на списки, например:
void Split_Polygon (polygon *poly, plane *part, list *&front, list *&back)
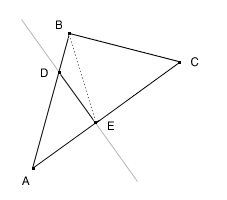
     2. Для данного случая (см.рис.) если вершины треугольника передавались в порядке их следования по часовой стрелке (то есть A,B и C), то процедура выдаст следующий результат:
outpts[] = E, A, D
inpts[] = E, D, B, C
     3. Таким образом простейшим способом деления четырехугольника на треугольники с сохранением заданной ориентации будет выборка 1-й, 2-й и 3-й вершин для первого треугольника и 1-й, 3-й и 4-й вершин для второго треугольника, то есть в нашем случае по одну сторону от плоскости будет лежать треугольник EAD, а по другую - треугольники EDB и EBC.

     4. Также необходимой будет и модификация основной процедуры Build_BSP_Tree() для того, чтобы она могла принимать несколько полигонов для добавления в узлы из функции Split_Polygon().

4. Применение BSP-дерева для удаления скрытых поверхностей

Обзор

     Возможно самым частым применением BSP-деревьев является удаление скрытых поверхностей в трех измерениях. Эти структуры данных обеспечивают быстрый и "безболезненный" метод отбора и сортировки полигонов путем рекурсии по дереву. Этот факт мы сейчас и используем "пересмотрев" методы удаления невидимых граней и расширив их при помощи BSP-дерева.

Оптимизация алгоритма художника

     BSP-деревья идеально подходят для реализации алгоритма художника, так как процесс разделения полигонов есть изначальный процесс создания BSP-дерева. Все что остается сделать после создания сцены и ее BSP-дерева - это рекурсивно пройти его "от передних ветвей к задним" (back-to-front traversal). Делается это так:
     1. Начав с корневого узла дерева, определить положение камеры (eye point) относительно делящей плоскости этого узла.
     2. Прорисовать сначала противоположную ветвь, потом полигоны, принадлежащие делящей плоскости, ну и наконец ветвь, в которой находится камера.
     3. Повторять этот процесс рекурсивно для каждого узла дерева.

Z-буфер, scanline-метод

     Эти методы используют другой подход - им требуется прорисовка от передних плоскостей к задним, что также возможно при помощи BSP-дерева, только называется это front-to-back traversal. Делается так:
     1. Начав с корневого узла дерева, определить положение камеры (eye point) относительно делящей плоскости этого узла.
     2. Прорисовать сначала ветвь, в которой находится камера, потом полигоны, принадлежащие делящей плоскости, ну и наконец противоположную ветвь.
     3. Повторять этот процесс рекурсивно для каждого узла дерева.

Замечания

     При построении BSP-дерева для удаления невидимых поверхностей делящие плоскости почти всегда выбираются из входящих в сцену полигонов. Однако, любая плоскость может быть использована как делящая, что наверняка приведет к положительному скачку в производительности генератора BSP-дерева и программы в целом.

Псевдокод

     Вот небольшой пример рекурсивного прохода дерева от задних ветвей к передним (back-to-front):

void    Draw_BSP_Tree (BSP_tree *tree, point eye)
{
real result = tree->partition.Classify_Point (eye);
if (result > 0)
{
Draw_BSP_Tree (tree->back, eye);
tree->polygons.Draw_Polygon_List ();
Draw_BSP_Tree (tree->front, eye);
}
else if (result < 0)
{
Draw_BSP_Tree (tree->front, eye);
tree->polygons.Draw_Polygon_List ();
Draw_BSP_Tree (tree->back, eye);
}
else // result is 0
{
// the eye point is on the partition plane...
Draw_BSP_Tree (tree->front, eye);
Draw_BSP_Tree (tree->back, eye);
}
}

     Если камера находится на делящей плоскости, то теоретически порядок прорисовки ветвей неясен. В этом случае мы не выводим на экран полигоны, принадлежащие плоскости, потому что их все равно не будет видно.
     Можно улучшить этот пример, если представлять камеру как направленный вектор: тогда мы сможем определять видимость отдельных ветвей, что в некоторых случаях даст 50%-й прирост скорости. Ветви, находящиеся позади камеры, можно будет просто не выводить на экран, а также поможет нам решить проблему выбора нужной ветви при нахождении игрока на делящей плоскости.
     Эта процедура легко переделывается под front-to-back traversal - достаточно просто поменять местами 4 строки: Какие? Если вы поняли, о чем велась речь, это не составит для вас труда.

5. Двоичные операции при помощи BSP-деревьев

     Раздел в пока процессе разработки
В принципе он уже готов
Если кому срочно надо - пишите

6. Исходные коды, готовые программы и примеры

     Раздел в пока процессе разработки
C++ - не готов еще
Delphi - аналогично
Visual basic - тоже